Are you desperately looking for 'how to write in y a xh 2 k'? Here you can find all of the details.
Table of contents
- How to write in y a xh 2 k in 2021
- Vertex form calculator
- Y=a(x-h)^2+k examples
- A(x-h)^2+k calculator
- Vertex form
- Y=a(x-h)^2+k how to find a
- Y=a(x-h)^2
- Standard form to vertex form
How to write in y a xh 2 k in 2021
This image demonstrates how to write in y a xh 2 k.
Vertex form calculator
This image shows Vertex form calculator.
Y=a(x-h)^2+k examples
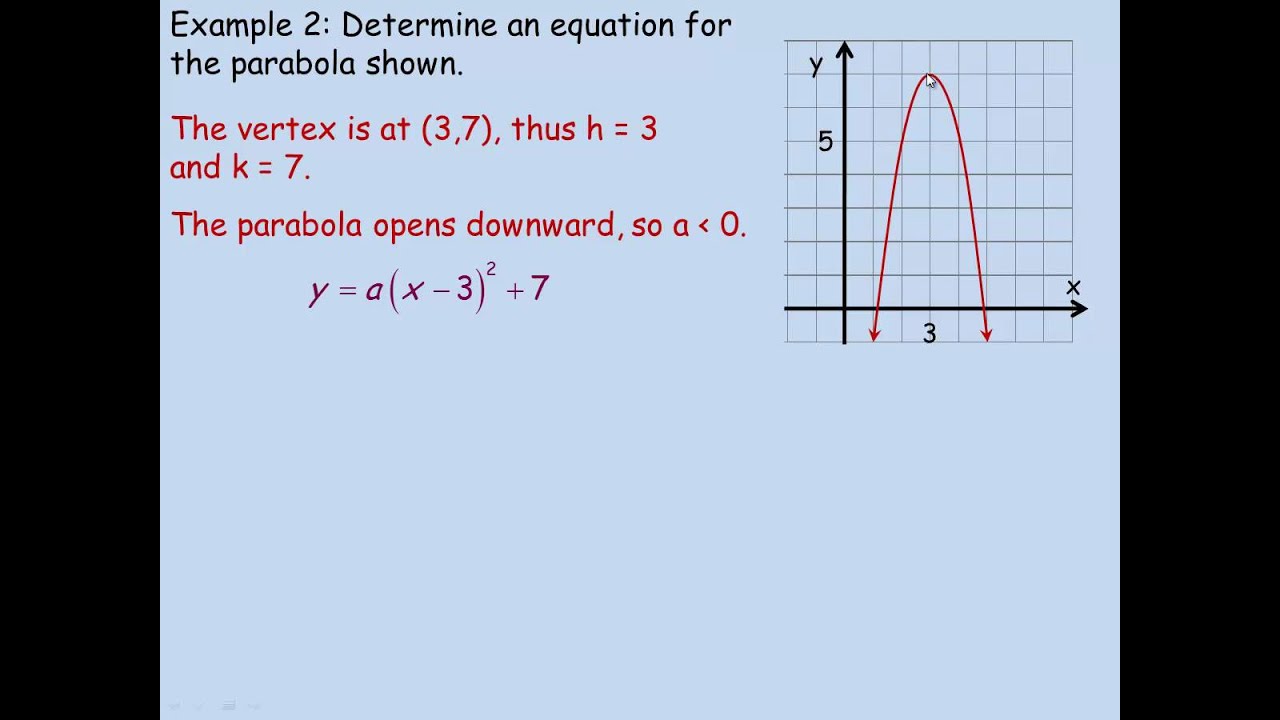This image representes Y=a(x-h)^2+k examples.
A(x-h)^2+k calculator
This image representes A(x-h)^2+k calculator.
Vertex form
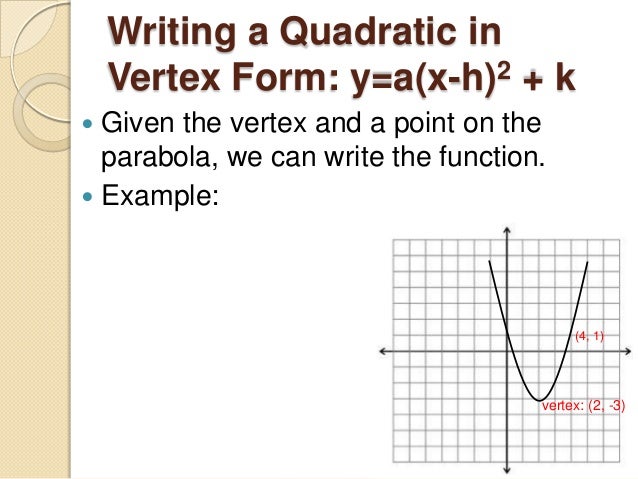This picture illustrates Vertex form.
Y=a(x-h)^2+k how to find a
This image shows Y=a(x-h)^2+k how to find a.
Y=a(x-h)^2
This picture demonstrates Y=a(x-h)^2.
Standard form to vertex form
This image illustrates Standard form to vertex form.
How to write a solution for the equation IE?
Practice! You can put this solution on YOUR website! Take half of the x coefficient to get (ie ). Now add and subtract this value inside the parenthesis. Doing both the addition and subtraction of does not change the equation Now the quadratic is in vertex form where , , and . Remember (h,k) is the vertex and "a" is the stretch/compression factor.
Which is the correct way to multiply a by H?
Use the distributive property to multiply a by x^ {2}-2xh+h^ {2}. Use the distributive property to multiply a by x 2 − 2 x h + h 2. Swap sides so that all variable terms are on the left hand side. Swap sides so that all variable terms are on the left hand side. Subtract k from both sides. Subtract k from both sides. Combine all terms containing a.
How to write the equation y with the given?
SOLUTION: write the equation y=a (x-h)^2+k with the given. with a y-intercept 10, x-intercept 2, and equation of axis x-3=0 Practice! Question 274307: write the equation y=a (x-h)^2+k with the given.
How to solve X 2 H 2 K?
Divide both sides by x^ {2}-2xh+h^ {2}. Divide both sides by x 2 − 2 x h + h 2. Dividing by x^ {2}-2xh+h^ {2} undoes the multiplication by x^ {2}-2xh+h^ {2}. Dividing by x 2 − 2 x h + h 2 undoes the multiplication by x 2 − 2 x h + h 2.
Last Update: Oct 2021